Sinc interpolation is a special case of sinc filtering, which is a method of removing all harmonics from a sound above a certain cutoff frequency and leaving all other harmonics untouched (I'm not totally sure, but I believe harmonics exactly at the cutoff frequency have their amplitudes halved). I don't fully understand why it works, but here's how it works:
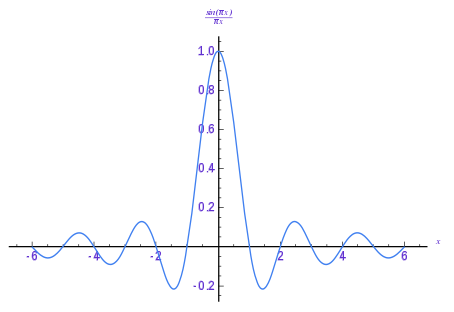
A sinc filter is a filter whose impulse response function is the normalized sinc function:
sinc(x)=...
if x=0: 1
if x!=0: sin(pi*x)/(pi*x)
which looks like this:
Note that, mathematically, a filter is a transformation on a function (like differentiation and integration) that has certain special properties. The impulse response function of a filter is the function that results from performing the transformation on the impulse function (an infinitely thin, infinitely tall spike at x=0, and zero everywhere else).
Given a filter with impulse response function ir(x), you can transform f(x) into g(x) in the following way:
In digital audio, a waveform consists of a bunch of discrete points, so when you "integrate", all you're really doing is multiplying the height of each point by the appropriate value in the IRF, and adding them all up.
Many filters have finite impulse response, meaning that only a finite portion of the IRF is nonzero, so you don't actually have to integrate from negative infinity to infinity, only over the nonzero portion of the IRF. The sinc function, however, has an infinite nonzero portion, so you can't truly program a computer integrate over the entire function, as that would take infinitely long. The best you can do is approximate by using some portion of the function like -10 to 10 or -100 to 100 or something like that.
Generally speaking, audio interpolation is something that must be done any time you want to play an audio sample and it involves examining the waveform between sample frames rather than on sample frames (it essentially converts the set of discrete points to a continuous function). The simplest way is to round to the nearest sample frame (nearest neighbor interpolation). The next simplest way is to play "connect the dots" with the sample frames (linear interpolation). There are others, but sinc interpolation is the theoretical ideal (though, as mentioned before, it's impossible to implement perfectly due to the need for an infinite integral) as it (theoretically) produces no aliasing (introduction of new frequencies) unlike the others, and is therefore also known as "anti-aliasing".
Sinc interpolation converts the discrete set of points in a digital audio sample to a continuous function by applying the sinc filter to the function consisting of an impulse of the appropriate height (which is technically infinite) at every sample frame.
For example, suppose the digital audio sample f(x) consisted of the following 3 sample frames:
f(0)=1
f(1)=-1
f(2)=2
The corresponding continuous function, as derived with sinc interpolation, would be:
g(x)=1*sinc(0-x) + -1*sinc(1-x) + 2*sinc(2-x)



 . Also, in this image:
. Also, in this image: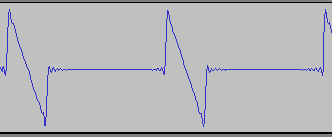
 .
.

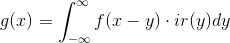

 .
.