The Quest for a Calculator
The Doctor is in dire need of a calculator, but due to budget cuts, he asks Misery and Balrog to build one for him.
Balrog comes up with a counting machine. It's in the early stages, so it can only hold 10 different kinds of numbers: the digits 0 through 9.
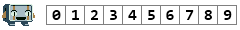
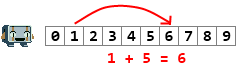
Balrog can use his simple calculator to add and subtract numbers. For example, he can evaluate the expression 1 + 5.
This machine works fine, but it has one major flaw: there are no negative numbers. Misery steps in and creates her own counting machine.
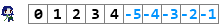
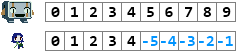
She's invented a strange system. For some reason, negative 5 comes right after positive 4. She still only has 10 slots to work with, and she needs support for both negative and positive numbers.
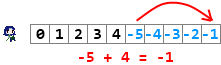
Now Misery is able to do math with negatives.
Balrog claims that his machine is better because the maximum positive number is 9, not 4. However, Misery argues the opposite. She asks him, "If I add 1 to 9, what do I get?". Balrog realizes his machine doesn't support the number 10 yet, so he has to make his number chart "wrap around". He says the answer is 0. After adding 1 to the biggest possible number, his machine overflows and resets to the smallest number (which is 0 in his case). Balrog's answer is not true because 9 + 1 is not zero.
Instead of having the number 9, Misery has -1 in its place. If she adds 1 to her machine, the -1 will overflow. Even so, it will overflow to 0. Of course, -1 + 1 = 0, so her machine would still be right.

When overflowing past 0, Misery's machine does not suffer from the same kind of problem as Balrog's machine. She can do -5 + 7 without any problems, and her machine will be correct.
The Doctor points out an issue. Misery's counting machine suffers from a different kind of overflow. When you add 1 to 4, you get -5. This is not right, because positive 5 is the right answer. In this case, Balrog's machine would be correct (1 + 4 = 5), but Misery's would be incorrect.
In the end, the Doctor decides to accept both methods of representing numbers, since both Balrog's method and Misery's method have their advantages. He calls Balrog's system unsigned numbers, because none of Balrog's numbers have a negative sign. He calls Misery's system signed numbers, because some of Misery's numbers have negative signs.
Signed and Unsigned Numbers in ASM
I told you that every 32-bit register (EAX, ECX, EDX...) can hold a maximum of 8 hex digits. You can't hold more than 8 hex digits, so that implies that these registers have a maximum value and a minimum value.
That is true. However, the maximum/minimum values will be different depending on whether we interpret numbers as signed or unsigned.
Unsigned Numbers (Balrog's Method)
|
We see that for EAX, ECX, EDX, and all those other 32-bit registers, the maximum decimal value is slightly less than 4.3 billion.
For AX, CX, DX, and so on, the maximum decimal value is about 65 thousand. For AL, AH, CL, and so on, the maximum decimal value is a measly 255.
Signed Numbers (Misery's Method)
|
If we interpret all numbers as signed instead of unsigned, we see that the maximum for a 32-bit register is about 2.1 billion, and the minimum is about -2.1 billion.
The max for a 16-bit register is about 32 thousand. The minimum is about -32 thousand.
For 8-bit registers, the max is 127 and the minimum is -128.
Be careful while using these two tables. The minimum value of a register while using the signed method is NOT the same as the minimum value of a register while using the unsigned method. This is obvious if you think about it. The min value for an unsigned DWORD-sized register is 0. The min value for a signed DWORD-sized register is -80000000 (hex), or -2147483648 in decimal. Clearly, 0 is not equal to -2147483648.
Clarifying Unsigned and Signed Numbers
EAX is 0. (I'm using the unsigned method).
If I switch over to the signed method, then what is EAX? Is it -80000000?
Of course not. I told you earlier that this wasn't true. Look at Misery's counting machine and Balrog's counting machine. Both of them contain the number 0, and in each case the number 0 is the first slot of the number chart. In both unsigned and signed notation, EAX is still 0.
To make things as clear as possible, I'll give you a list of numbers, with their signed and unsigned equivalents.
Here we assume the data size is 32-bits.
Unsigned Signed 0 0 18 18 FFFFFFFF -1 FFFFFE00 -200 8950ABCD -76AF5433 500 500 10999 10999 ABCDEF ABCDEF 7FFFFFFF 7FFFFFFF 80000000 -80000000You may find it interesting that in unsigned notation, 80000000 is the same thing as -80000000 in signed notation. It seems strange at first, but it makes perfect sense. In the counting machines, Balrog had the number positive 5, yet Misery had the number -5 in the same corresponding slot. If we make both those machines much wider, then we could envision the hex number 80000000 (Balrog's number) being in the same corresponding slot as Misery's hex number -80000000.
In ASM, notice that Misery's signed number system can still hold large positive values, up to 7FFFFFFF in hex. Balrog can hold even bigger positive numbers, up to FFFFFFFF. The restriction is that Balrog cannot represent any negative numbers, while Misery can represent negatives as low as -80000000 in hex.
Registers also "wrap around" just like the counting machines. If you're using Balrog's method and you add the number 1 to FFFFFFFF, you will get 0 because the register cannot fit 9 hex digits. Instead of causing an error message, the register just resets back to 0.
MOV EAX,FFFFFFFF INC EAX ;EAX is now 0. MOV EAX,FFFFFFFF ADD EAX,8 ;EAX is now 7, because FFFFFFFF can be treated just like -1.
Previous Lesson: Redefining Memory
Next Lesson: Redefining Jumps
Table of Contents